ضرایب همبستگی و آزمونهای معناداری
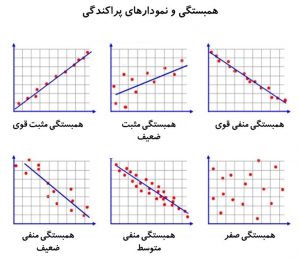
در تحلیلهای آماری، ارتباطات بین متغیرها و بررسی معناداری این ارتباطات از اهمیت ویژهای برخوردار است. با استفاده از روشهای مختلف، میتوانیم به بررسی و تحلیل روابط میان دادهها پرداخته و نتایج قابل استنادی بدست آوریم. یکی از ابزارهای اصلی در این فرآیند، استفاده از ضرایب همبستگی و آزمونهای معناداری است که به ما امکان میدهد تا ارتباطات موجود را با دقت بیشتری ارزیابی کنیم.
ضرایب همبستگی، ارتباط بین دو یا چند متغیر را اندازهگیری کرده و نشان میدهند که چقدر تغییرات یکی از متغیرها با تغییرات دیگری همراستا است. آزمونهای معناداری نیز به ما این امکان را میدهند که بررسی کنیم آیا نتایج بهدستآمده تصادفی هستند یا اینکه ارتباط موجود دارای ارزش علمی و معتبر است.
این مفاهیم ابزارهای قدرتمندی در تحلیل دادهها به شمار میروند و با استفاده درست از آنها میتوانیم به نتایج معناداری دست یابیم که در تحقیقات علمی، تصمیمگیریها و پیشبینیها کاربرد فراوانی دارند.
تعریف ضرایب همبستگی
ضرایب همبستگی ابزارهایی هستند که برای اندازهگیری ارتباط بین دو یا چند متغیر استفاده میشوند. این ضرایب نشان میدهند که چقدر تغییرات در یک متغیر با تغییرات در متغیر دیگر هماهنگ است. در تحلیلهای آماری، فهم روابط میان دادهها از اهمیت زیادی برخوردار است و ضرایب همبستگی به تحلیلگران این امکان را میدهند تا درک دقیقتری از ارتباطات موجود پیدا کنند.
انواع ضرایب همبستگی
- ضریب همبستگی پیرسون: این ضریب برای سنجش ارتباط خطی میان دو متغیر استفاده میشود. مقدار آن بین -1 و 1 قرار دارد.
- ضریب همبستگی اسپیرمن: این ضریب برای اندازهگیری همبستگی رتبهای و غیرخطی به کار میرود.
- ضریب همبستگی کندال: مشابه اسپیرمن است، ولی برای دادههای مختلف و پیچیدهتر به کار میرود.
کاربردهای ضرایب همبستگی
- شناسایی روابط مثبت و منفی بین متغیرها
- پیشبینی رفتار یک متغیر بر اساس تغییرات متغیر دیگر
- تحلیل ساختار دادهها و تعیین ارتباطات در تحقیقات علمی
مفاهیم و کاربردهای اصلی
در تحلیلهای آماری، مفاهیم مربوط به ضرایب همبستگی و آزمونهای معناداری نقش اساسی در فهم روابط میان متغیرها دارند. این مفاهیم به تحلیلگران کمک میکنند تا روابط مختلف در دادهها را شناسایی کرده و تأثیرات این روابط را بر نتایج تحقیق و پیشبینیها ارزیابی کنند. فهم دقیق این مفاهیم میتواند به بهبود دقت تحلیلها و تصمیمگیریهای آماری کمک کند.
کاربردهای اصلی این ابزارها در زمینههای مختلف تحقیقاتی و صنعتی شامل شناسایی الگوهای پنهان در دادهها، تحلیل اثرات متغیرهای مختلف بر یکدیگر و پیشبینی رفتار سیستمها در شرایط مختلف است. به کمک ضرایب همبستگی، میتوان روابط مستقیم و غیرمستقیم میان متغیرها را اندازهگیری کرده و از این اطلاعات برای انجام آزمونهای معناداری استفاده کرد.
انواع ضرایب همبستگی
در تحلیلهای آماری، برای اندازهگیری و ارزیابی ارتباط میان متغیرها از انواع مختلفی از ضرایب همبستگی استفاده میشود. این ضرایب بسته به نوع دادهها و نوع ارتباط میان آنها میتوانند متفاوت باشند. انتخاب مناسبترین ضریب همبستگی برای تحلیل یک مجموعه داده، به دقت تحلیل و نتایج صحیحتری منجر میشود.
برخی از مهمترین انواع ضرایب همبستگی که در تحقیقهای آماری کاربرد دارند، شامل ضریب همبستگی پیرسون برای دادههای پیوسته و خطی، ضریب همبستگی اسپیرمن برای دادههای رتبهای و ضریب همبستگی کندال برای بررسی ارتباط میان دادههای غیرخطی میباشند. هر یک از این ضرایب ویژگیها و کاربردهای خاص خود را دارند که در ادامه به بررسی آنها پرداخته خواهد شد.
کوری، پیرسون و اسپیرمن
در تحلیلهای آماری، برای اندازهگیری همبستگی میان متغیرها از روشهای مختلفی استفاده میشود. هر یک از این روشها بسته به نوع دادهها و نوع ارتباط میان آنها، ویژگیهای متفاوتی دارند. سه روش مهم و پرکاربرد در این زمینه، روشهای کوری، پیرسون و اسپیرمن هستند که در تحلیلهای مختلف استفاده میشوند.
ضریب همبستگی کوری
ضریب همبستگی کوری برای اندازهگیری همبستگی بین دو متغیر رتبهای به کار میرود. این روش بیشتر زمانی مفید است که دادهها بهصورت غیرخطی یا نامتقارن توزیع شده باشند. ضریب کوری، بهویژه در بررسی دادههایی که توزیع نرمال ندارند، کاربرد فراوانی دارد.
ضریب همبستگی پیرسون
ضریب همبستگی پیرسون، یکی از رایجترین ضرایب همبستگی است که برای دادههای پیوسته و خطی استفاده میشود. این ضریب میزان ارتباط خطی میان دو متغیر را اندازهگیری کرده و مقادیر آن بین -1 و 1 قرار دارد. ضریب 1 به معنی ارتباط کامل مثبت و ضریب -1 نشاندهنده ارتباط کامل منفی است. ضریب صفر نشاندهنده عدم وجود ارتباط است.
ضریب همبستگی اسپیرمن
ضریب همبستگی اسپیرمن، مشابه ضریب پیرسون است، اما بهجای استفاده از دادههای پیوسته، این روش برای دادههای رتبهای به کار میرود. این ضریب برای اندازهگیری ارتباط غیرخطی و رتبهای میان دو متغیر مناسب است. این روش زمانی کاربرد دارد که دادهها خطی نباشند یا در مقیاس رتبهای اندازهگیری شده باشند.
آزمون معناداری چیست؟
آزمون معناداری ابزاری است که در تحلیلهای آماری برای ارزیابی صحت نتایج و ارتباطات میان متغیرها استفاده میشود. این آزمونها به ما این امکان را میدهند که تعیین کنیم آیا یک نتیجه تصادفی است یا دارای اعتبار علمی و قابل استناد میباشد. هدف اصلی این آزمونها، تشخیص معناداری تفاوتها و روابط موجود در دادهها است تا بتوانیم از آنها برای تصمیمگیریهای آماری بهرهبرداری کنیم.
آزمونهای معناداری بهطور معمول با استفاده از فرضیههای آماری انجام میشوند که در آنها فرضیه اولیه (فرضیه صفر) و فرضیه جایگزین مورد بررسی قرار میگیرند. نتیجه آزمون معناداری میتواند نشان دهد که آیا دادهها با احتمال زیاد از یک مدل یا فرضیه خاص پیروی میکنند یا خیر.
نحوه تشخیص نتایج معنادار
تشخیص نتایج معنادار یکی از مراحل کلیدی در تحلیلهای آماری است که به ما این امکان را میدهد تا از صحت و اعتبار نتایج بهدستآمده اطمینان حاصل کنیم. این فرآیند شامل بررسی این است که آیا ارتباطات و تفاوتهای مشاهدهشده در دادهها تصادفی هستند یا اینکه دارای ارزش علمی و واقعی میباشند. با استفاده از آزمونهای معناداری میتوانیم تعیین کنیم که آیا نتایج بهطور تصادفی بهدستآمدهاند یا بهطور قطعی ارتباط یا تفاوت معناداری وجود دارد.
سطح معناداری و ارزش p
برای تشخیص نتایج معنادار، یکی از مهمترین معیارها، مقدار p است. این مقدار نشاندهنده احتمال آن است که نتایج بهدستآمده تنها بهطور تصادفی رخ داده باشند. هرگاه مقدار p کمتر از سطح معناداری معین (معمولاً 0.05) باشد، فرضیه صفر رد میشود و نتیجه بهعنوان معنادار در نظر گرفته میشود.
خطای نوع اول و نوع دوم
در فرآیند آزمون معناداری، دو نوع خطا وجود دارد که باید به آنها توجه کرد: خطای نوع اول و خطای نوع دوم. خطای نوع اول زمانی رخ میدهد که فرضیه صفر به اشتباه رد شود، در حالی که در واقع ارتباط یا تفاوت معناداری وجود ندارد. خطای نوع دوم زمانی اتفاق میافتد که فرضیه صفر به اشتباه رد نشود، در حالی که در واقع ارتباط یا تفاوت معناداری وجود دارد. توجه به این خطاها در تعیین نتایج معنادار ضروری است.
رابطه بین ضرایب همبستگی و معناداری
ضرایب همبستگی و آزمونهای معناداری ارتباط نزدیکی با یکدیگر دارند و در کنار هم به تحلیلگر کمک میکنند تا صحت نتایج و روابط میان متغیرها را ارزیابی کند. در واقع، ضرایب همبستگی بهطور مستقیم نشاندهنده شدت و نوع ارتباط بین متغیرها هستند، در حالی که آزمونهای معناداری به بررسی این میپردازند که آیا این ارتباطات بهطور تصادفی بهدستآمدهاند یا واقعاً معتبر و معنادار هستند. با استفاده از هر دو ابزار میتوان به نتیجهگیریهای دقیقتری دست یافت.
تأثیر ضرایب همبستگی بر آزمونهای معناداری
مقدار ضرایب همبستگی میتواند در تفسیر نتایج آزمونهای معناداری نقش مهمی ایفا کند. ارتباط قوی میان دو متغیر معمولاً احتمال رد فرضیه صفر و دستیابی به نتیجه معنادار را افزایش میدهد. از سوی دیگر، ضرایب همبستگی ضعیف یا صفر میتواند نشاندهنده آن باشد که ارتباط قابلتوجهی بین متغیرها وجود ندارد و نتیجه آزمون معناداری احتمالاً نشاندهنده عدم وجود ارتباط است.
مقایسه ضرایب همبستگی با نتایج آزمونهای معناداری
| ضریب همبستگی | نتیجه آزمون معناداری | تفسیر |
|---|---|---|
| 0.9 یا بیشتر | معنادار | ارتباط قوی و معنادار بین متغیرها |
| 0.5 تا 0.9 | معنادار | ارتباط متوسط تا قوی، احتمال معناداری بالا |
| 0.1 تا 0.5 | غیر معنادار | ارتباط ضعیف، احتمال معناداری کم |
| 0 یا نزدیک به صفر | غیر معنادار | عدم وجود ارتباط قابل توجه |
چگونگی تاثیرگذاری بر تحلیل دادهها
ضرایب همبستگی و آزمونهای معناداری میتوانند تأثیرات مهمی بر روند تحلیل دادهها داشته باشند. این ابزارها به تحلیلگران کمک میکنند تا روابط میان متغیرها را شناسایی کرده و نتایج آزمونها را بهطور علمی ارزیابی کنند. انتخاب صحیح این ابزارها و استفاده بهموقع از آنها میتواند باعث بهبود دقت تحلیلها و پیشبینیهای انجامشده گردد.
- تعیین ارتباطات موجود: استفاده از ضرایب همبستگی میتواند به شناسایی ارتباطات مستقیم و غیرمستقیم میان متغیرها کمک کند.
- تحلیل نتایج آزمونهای معناداری: این آزمونها به تحلیلگران امکان میدهند تا بررسی کنند که آیا ارتباطات بهدستآمده ناشی از تصادف هستند یا واقعی و معتبر هستند.
- ارزیابی صحت تصمیمات: تحلیلهای دقیق و استفاده از ابزارهای معناداری میتواند به کاهش خطاهای تصمیمگیری و ارزیابی دقیقتر کمک کند.
با تحلیل دقیقتر دادهها، تحلیلگران قادر خواهند بود تا نتایج قویتری ارائه دهند و ارتباطات و روندها را بهطور بهتر شبیهسازی کنند. این فرآیند در زمینههای مختلف از جمله تحقیقات علمی، پیشبینیهای اقتصادی و تصمیمگیریهای کسبوکار قابلاستفاده است.